If you have a Python project, Cython is an indespensible skill.
Cython is a Python-like language that adds C extensions to your Python project. For when you want to write Python, but need turbocharge some slow execution path by compiling it to native code.
Inspired to improve SearchArray, I bought a copy of Kurt Smith’s Cython: A Guide For Programmers with a goal of improving SearchArray’s biggest bottleneck: sorted array intersections.
Intersecting sorted arrays
SearchArray relies on intersecting sorted arrays. In its search index, SearchArray encodes term positions using a roaring-bitmap like approach. For example, consider these documents:
doc1: ... Mary had a little lamb ...
doc4: That little lamb is named Mary ...
Term little here would be encoded like below:
little: 0001 0004 0001 0000
^^^^ ^^^^ ^
docid | |
+-- Payload MSB -- what positions we're storing here (here doc1's 4*16 = 64th posn)
|
+-- 5th posn after 4*16
A header holds the doc ids and the most-significant bits of its term positions (a region of positions). Then the remaining 16 bit payloads represent the positions occupied by this term. In the example above, we’re representing the locations between positions 4*16 to (4*16)-1 that we can find the term little.
And this being an inverted index, we keep all of little’s positions, across all docs it occurs in, in one big array:
little: 0001 0004 0001 0000 | 0001 0008 ... ... | 0004
^^^^ ^^^^ ^ ^^^^ ^^^^ ^^^^
doc 1 | | posns in doc 1, starting at 8*16 posns for doc 4
+-- Payload MSB -- what positions we're storing here (here doc1's 4*16 = 64th posn)
|
+-- 5th posn after 4*16
This sorted array of little’s positions can be intersected with lambs for regular AND search, just by intersecting the doc ids:
little: 0001 0004 0001 0000 | 0001 0008 ... ... | 0004
lamb: 0001 0004 .... .... | 0004 ....
Intersected doc ids: [0001, 0004]
Alternatively, for phrase search, ie "little lamb" we intersect doc ids and position MSBs to get nearby positions of both terms. Then look for adjacent bits across those intersected locations. More about that in the roaringish blog article.
Optimizing Roaringish with faster sorted intersections
Roaringish’s bottleneck is intersecting the sorted array headers. As these are numpy arrays, you might think numpy’s built in intersection would just work for this use case. Unfortunately intersect1d is not focused on sorted data, it’s meant to be general purpose intersection of arrays.
Two-pointer algorithm
Intersecting sorted data ought to be faster, as you can walk each array with the two-pointer algorithm.
Let’s call our two arrays lhs and rhs. Start an index (lhs_idx and rhs_idx) at each array’s beginning. We can simply increment whichever location is before the other. If they’re equal though, you’ve found an intersection:
output = []
while lhs_idx < end_lhs and rhs_idx < end_rhs:
if lhs[lhs_idx] < rhs[rhs_idx]:
lhs_idx += 1
elif rhs[rhs_idx] < lhs[lhs_idx]:
rhs_idx += 1
else: # They're equal, this is an intersection!
# Collect intersected values
output.append(lhs[lhs_idx])
One problem with this code - you can get stuck in a region with a lot of lhs before rhs. Meaning you’ll do a lot of lhs_idx += 1 over and over. Consider the array below w/ * indicating the currend index.
lhs: 1* 2 3 4 5 6 7 8 9 10 11 ... 599 600
rhs: 600* 7 8
It sure would be nice to blow past this giant region in lhs, jumping to that 600 that actually intersects!
Instead of scanning one at a time, what if we could accelerate scanning LHS, skipping over giant non-intersecting regions.
This idea is known as exponential or galloping search. It’s what Frank Sauerburger’s great sortednp library does. Instead of +=1, Frank’s library does +=(bigvalue) and backtracks if it gone too far. This bigvalue will double each loop, meaning you’ll quickly breeze past this giant region of uninteresting, non-intersecting data on lhs.
Such as this galloping function to find target in arr starting at idx:
def gallopping_search(arr, idx, target):
delta = 1
prev = idx
# Gallop just past target
while arr[idx] < target
idx += delta
if idx >= len(arr):
# past end
idx = len(arr - 1)
break
delta *= 2
prev = idx
# Backtrack: Find target between prev and idx
return binary_search(arr, target=target start=prev, end=idx)
Modifying the intersection code to add our galloping utility:
output = []
while lhs_idx < end_lhs and rhs_idx < end_rhs:
if lhs[lhs_idx] < rhs[rhs_idx]:
lhs_idx = galloping_search(lhs, lhs_idx, target=rhs[rhs_idx])
elif rhs[rhs_idx] < lhs[lhs_idx]:
rhs_idx = galloping_search(rhs, rhs_idx, target=rhs[rhs_idx])
if lhs[lhs_idx] == rhs[rhs_idx]: # They're equal, this is an intersection!
# Collect intersected values
output.append(lhs[lhs_idx])
Frank’s to be commended, this is a big performance improvement on sorted data, as you can see in this Icicle graph which shows the result of profiling intersection over some randomly generated data (see benchmark here):
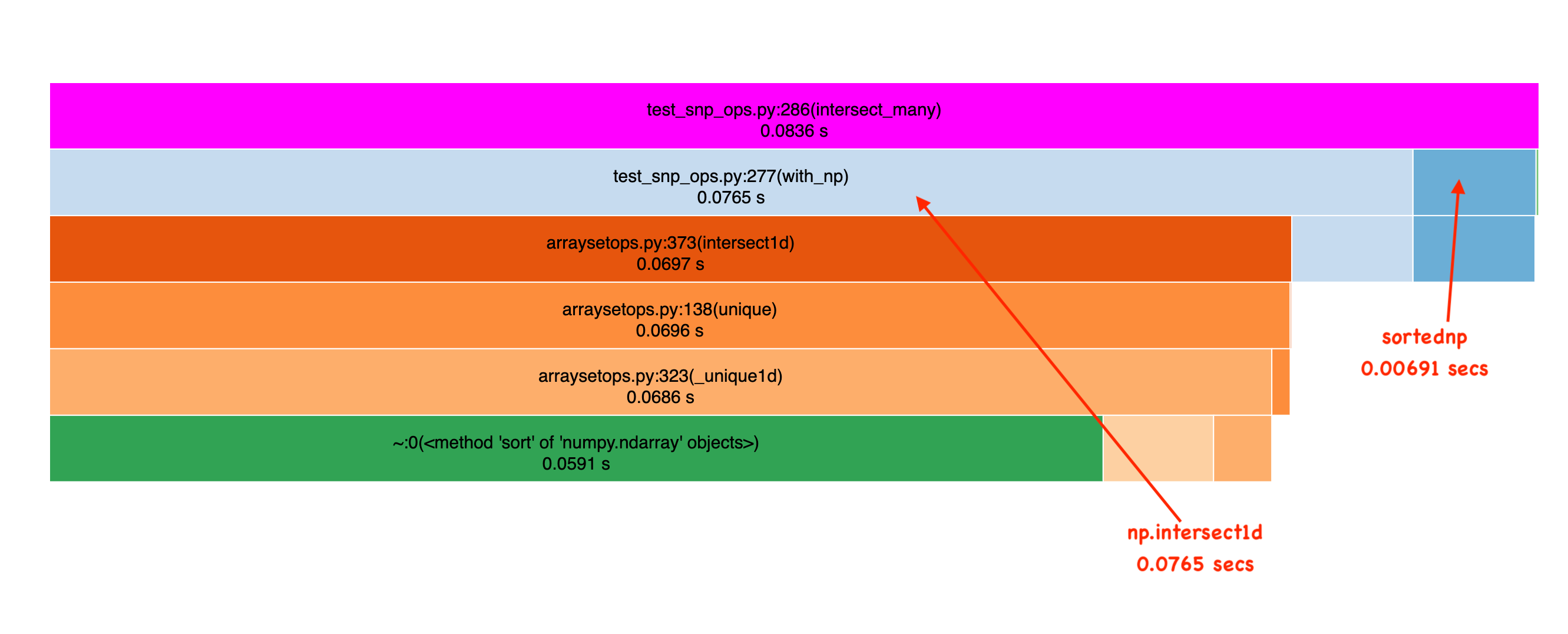
But for Roaringish this code is SUCH a bottleneck, that to make improvements, I had to obsess about performance at this layer. I have a couple of niche needs that just had to work very fast:
- I just care about unsigned integers, not generic data
- I need to mask as I go (I intersect a HEADER no the full value)
- Possibly my data has very specific patterns I could exploit
So I knew if I wrote very very tailored code, I could make improvements!
Cythonizing intersections
I wanted to sprinkle a tad bit of native code just in this one particular hotspot in my mostly Python code. So I reached for Cython to replace sortednp.
What is Cython exactly?
Cython lets you write Python code that gets compiled to a Python C extension. But it’s more than that.
Sure you can dump pure Python code in Cython, and it’ll get maybe 10% faster. However, more importantly, you can tell Cython to treat certain variables and functions like pure C, without all the dynamic typing etc - making your code friendlier for native performance, avoiding unexpected calls into the Python runtime. Walking through this code you’ll see what I mean.
My first step was just to port sortednp more-or-less directly into Cython. That parts a bit boring. What’s more fun is I kept going. Coming up with a pretty native friendly friendly approach to doing this galloping intersection.
Let’s walk through where I ended up to get a sense for how Cython works+helps.
C function w/ Python wrapper
The first thing you do when working with Cython is create a Python function as a wrapper:
def intersect(np.ndarray[DTYPE_t, ndim=1] lhs,
np.ndarray[DTYPE_t, ndim=1] rhs,
DTYPE_t mask=ALL_BITS):
# Validation, preparation etc
if mask is None:
mask = ALL_BITS
if mask == 0:
raise ValueError("Mask cannot be zero")
# Call C function
lhs_intesect, rhs_intersect = _gallop_intersect(lhs, rhs, ...)
# Massage output and return
return lhs_intersect, rhs_intersect
This is a Python function with all the bells and whistles, you can treat it like a Python object, pass it around, attach attributes to it, whatever. The only difference is the (optional) Cython type declarations before each variable. Two 1 dimensional numpy arrays, and a DTYPE_t (64 bit unsigned).
BUT declaring a special Cython cdef function lets you create a true C function:
cdef _gallop_intersect(DTYPE_t[:] lhs,
DTYPE_t[:] rhs,
DTYPE_t mask=ALL_BITS):
...
You’ll notice right away, some very different syntax for this cdef function.
You’ll also notice the syntax DTYPE_t[:] which indicates that we’re taking a memory view. Cython can directly convert numpy arrays this this memory view with zero copying! Memory views allow inspecting their dimensions through a shape attribute, etc much like numpy arrays. But they can also be interacted with like native C arrays, including index and pointer access.
Pre-allocating output and preparing for main loop
Within _gallop_intersect we need to prepare an output buffer. In this case, we know at most we can intersect the smaller of len(lhs) or len(rhs) values, so we allocate the output buffer accordingly. By preallocating the full output, we avoid the annoyances of managing dynamic arrays in our hot loop.
cdef _gallop_intersect(DTYPE_t[:] lhs,
DTYPE_t[:] rhs,
DTYPE_t mask=ALL_BITS):
...
cdef np.uint64_t[:] lhs_indices = np.empty(min(lhs.shape[0], rhs.shape[0]), dtype=np.uint64)
cdef np.uint64_t[:] rhs_indices = np.empty(min(lhs.shape[0], rhs.shape[0]), dtype=np.uint64)
This bit in the preamble is the one place in the C function we interact with the Python runtime – calling numpy to get an array. This is a bit safer than working with C’s heap directly (which we could do). I use Cython annotate to validate where I might inadvertantly interact with the Python runtime.
To return only a subset of this data, we track how much of the output is actually written. Then later, at the end of the function we can return just a slice of these arrays:
...
return np.asarray(lhs_indices)[:intersect_len], np.asarray(rhs_indices)[:intersect_len]
Again Python / Cython / Numpy are smarrt enough to do this kind of slice with no copying, just changing a size attribute of the underlying array object.
Boring C variables
Of course to walk these arrays we need some other items in our function
cdef _gallop_intersect(DTYPE_t[:] lhs,
DTYPE_t[:] rhs,
DTYPE_t mask=ALL_BITS):
# Current location in each
cdef DTYPE_t* lhs_ptr = &lhs[0]
cdef DTYPE_t* rhs_ptr = &rhs[0]
# End of each array
cdef DTYPE_t* end_lhs_ptr = &lhs[lhs.shape[0]]
cdef DTYPE_t* end_rhs_ptr = &rhs[rhs.shape[0]]
You’ll notice the cdef DTYPE_t* lets us interact with native pointers directly into each array. We save the end of the array and get pointers to the beginning of each. Cython dereferences array differently than a C programmer might expect - by doing lhs_ptr[0] instead of C’s *lhs_ptr.
Improving the galloping algorithm
Let’s walk through the actual code / algorithm. I’m omitting boring stuff, but you can see the full code here
What I realized was instead of galloping past, then searching between prev and after as in:
# Backtrack: Find target between prev and idx
return binary_search(arr, target=target start=prev, end=idx)
I could simplify the code path, and I felt speed up the code, by simply changing this line to something like
idx = prev + 1
Then checking if lhs / rhs were equal, collecting, and moving on.
So in other words, give up on the fancy binary search, trying to find the perfect, best possible intersecting spot between the before/after gallop. Instead entiriely rely on galloping and a simple check.
It seems dumber/slower. But a lot of times in native code, simple algorithms, interacting with fewer variables, and fewer branches perform better. Lots of branching means lots of times the CPU has to guess which code to load, and often it gets that wrong! Fewer branches, and a more linear code path leads to faster code with fewer headaches for your CPU.
Part one of such an approach would look something like this gallop w/ backtrack:
cdef np.uint64_t lhs_delta
cdef np.uint64_t rhs_delta
while lhs_ptr < end_lhs_ptr and rhs_ptr < end_rhs_ptr:
# Reset exponential search on each side
lhs_delta = 1
rhs_delta = 1
# ***************************
# Part 1 - Gallop LHS past the RHS, then backtrack
while lhs_ptr < end_lhs_ptr and (lhs_ptr[0] & mask) < (rhs_ptr[0] & mask):
lhs_ptr += lhs_delta
lhs_delta *= 2
# Backtrack by the previous delta
lhs_ptr = lhs_ptr - (lhs_delta // 2)
# Gallop RHS past LHS, then backtrack
while rhs_ptr < end_rhs_ptr and (rhs_ptr[0] & mask) < (lhs_ptr[0] & mask):
rhs_ptr += rhs_delta
rhs_delta *= 2
rhs_ptr = rhs_ptr - (rhs_delta // 2)
Followed by part two, a simple check to either increment one side by one, or collect an intersection:
# *********
# PART 2 NAIVE 2 pointer check
# Now that both sides are backtracked,
# we just do the naive 2-ptr check either incrementing one side by 1, or
#
if (lhs_ptr[0] & mask) < (rhs_ptr[0] & mask):
lhs_ptr += 1
elif (rhs_ptr[0] & mask) < (lhs_ptr[0] & mask):
rhs_ptr += 1
else: # INTERSECTION FOUND!
# Collect!
I hoped this code would be much easier for a C compiler / my CPU to run faster.
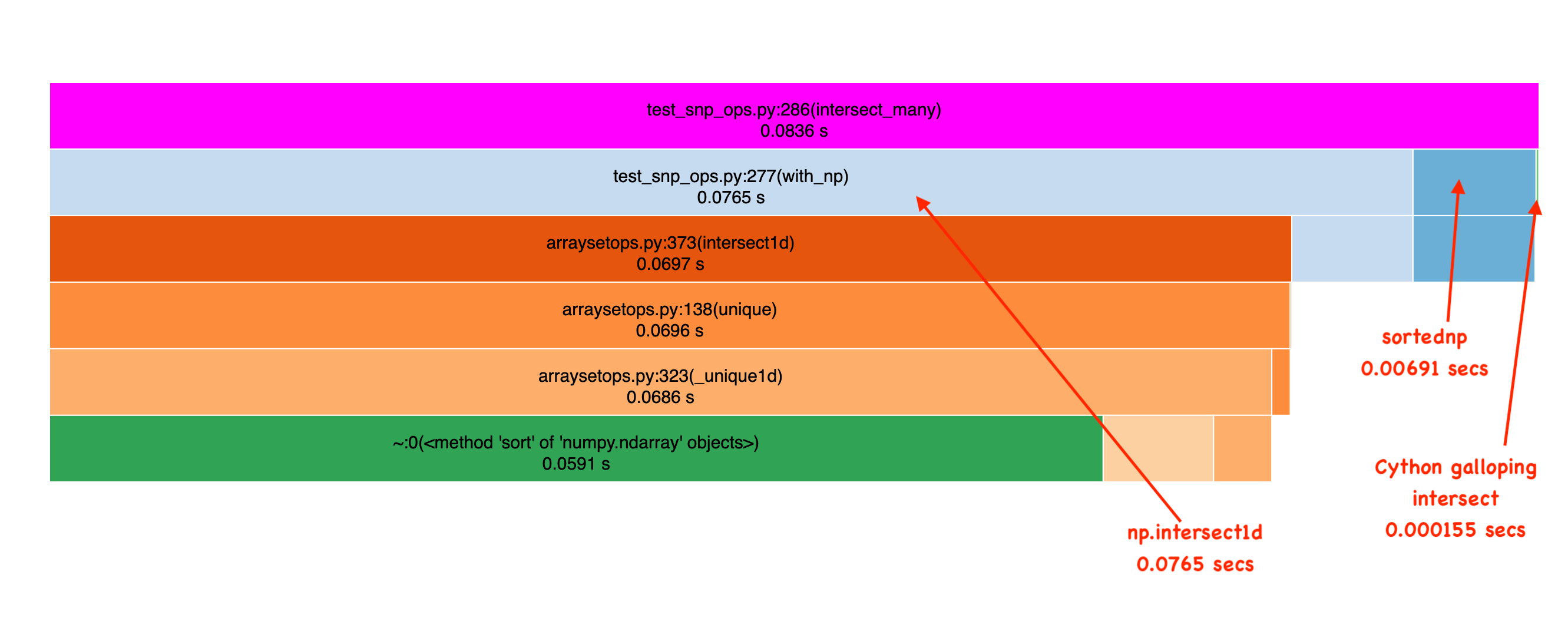
I was right!
Repeating the benchmarks above, I first see the order of magnitude improvement of sortednp over pure numpy. Nice! But look at our approach. It’s an order of magnitude faster still! Incredible!
I see this speedup in phrase search. Here, a fairly annoying phrase with very frequent terms:
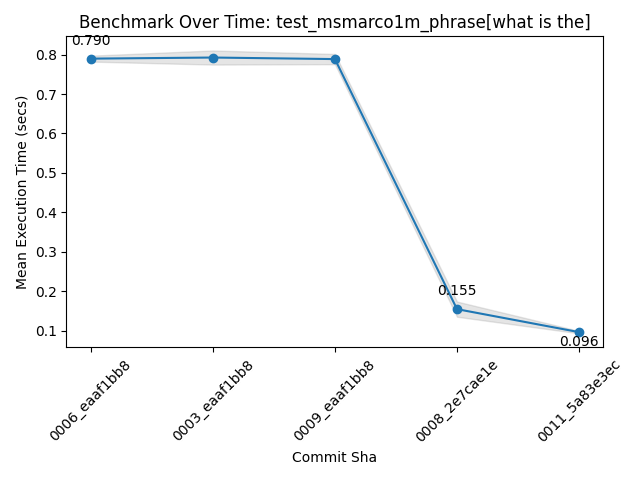
This search over 1 million (very beefy) MSMarco docs approaches the performance of this phrase on 100K docs a while back when I first introduced the roaringish approach. So making definite progress!
Nevertheless, running a profiler, we see for this benchmark intersections remain the bottleneck:
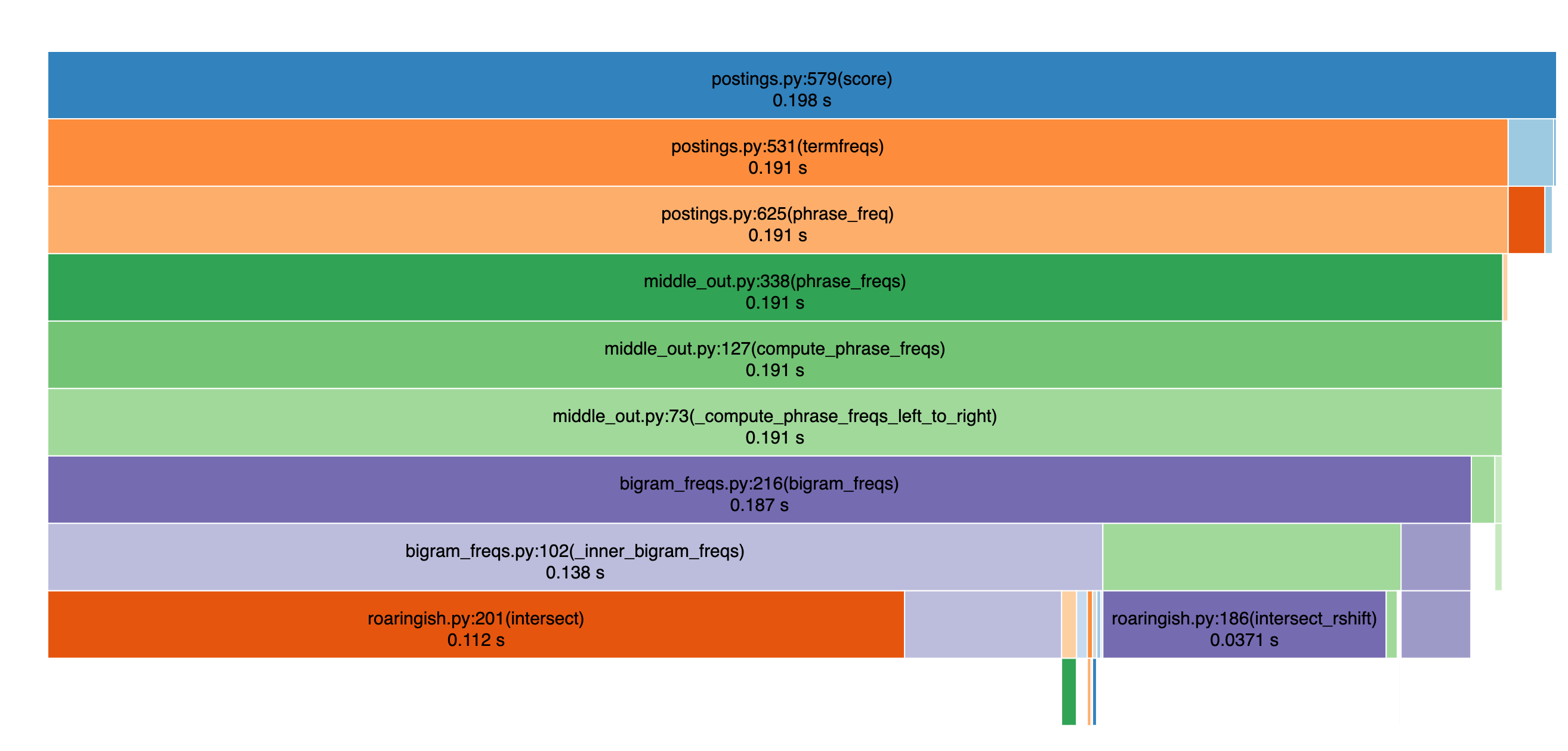
There’s work to do yet to make this really 100% usable for the full MSMarco corpus in memory (~3m docs), but it’s quickly getting there. I’m finding SearchArray indespensible prototyping information retrieval, RAG, search, etc ideas at the 100K doc scale. I’m hopeful SearchArray will become an obvious candidate for the 1m+ range soon!
There are some improvements I might consider:
- Putting the full phrase search algorithm in Cython - I search bigram-by-bigram in Python, intersecting as I go. I made an attempt at the full algorithm in Cython, trying to intersect in one pass. This attempt at this was actually slower, there’s reasons at the Python level just working with numpy array level abstractions / operations seems to work faster, as I can choose the rarer array to intersect first
- Looking at the full query plan - Currently many phrase searches are run in the context of a boost - on top of a baseline query. Why am I scoring things that might not match the original query? How can I filter these out?
- Threads / and friendlier for threads - I have not thought about how/if my algorithm would be threadsafe (at least for parallel searchers), and what implications this would have. I need to think about how Python’s global interpreter lock would play into attempting to parallelize searches.
Always more work to do! Enjoy SearchArray and give me feedback.
Enjoy softwaredoug in training course form!
 I hope you join me at Cheat at Search with LLMs to learn how to apply LLMs to search applications. Check out this post for a sneak preview.
I hope you join me at Cheat at Search with LLMs to learn how to apply LLMs to search applications. Check out this post for a sneak preview.
