Let’s say we have vectors A1..An. We know their dot products to u and v, but not u and v themselves. Can we estimate u.v (ie their cosine similarity)?
This could be handy in vector similarity systems. With just a few strategically selected reference points A1..An we might get an accurate view of u.v without storing the full vector. Or at least that’s the hope!
We first asked this question with just one reference point. Then we upgraded to two. Next we reach out with our feelings to get to all An reference points.
Recap - using two reference points
With just one reference point, we can estimate u.v with just u.A1 * v.A1. Easy enough.
To add a second, A2, we figure out how much of u.A2*v.A2 to include in u.v. We see how much of A2 is already included in the original reference point A1. The leftover parts parts, we add to u.v.
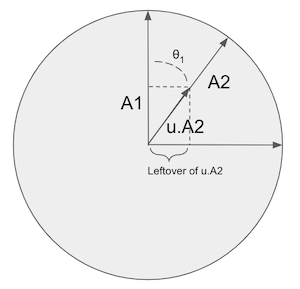
Applying the trig knowledge you told your teacher you’d never need, you know that ‘leftover’ here is really ‘sin’. So we get:
u.v = u.A1*v.A1 + sin(θ1)*u.A2*v.A2
Or put another way. if A1 and A2 are parallel, there’s no point in looking at the dot product u.A2 - it’s just u.A1 again. But as A2 rotates away, we add more and more of u.A2 in.
Up to 3 (or n) reference points
Going up to 3 (or n) dimensions, we need a similar procedure. However we need the leftovers of A3 outside the plane created by A1 and A2. That little slice of heaven shown below:
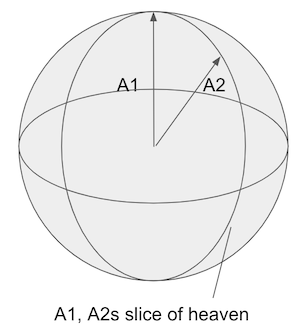
The mathy way of defining the “plane” where A1 and A2 lie (really any A1...An-1) is called a span.
The problem becomes, how do we find an angle, θ, between An - not on the span - and its closest point on the span A1...An-1.
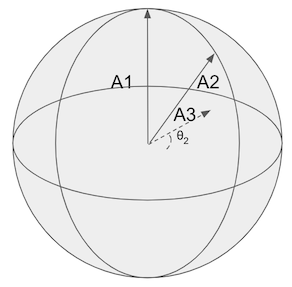
If we find θ we can add another + sin(θ)*u.An*v.An to the dot product and improve our estimate.
The ‘closest point’ of An on the span is known as a vector’s orthogonal projection, shown below:
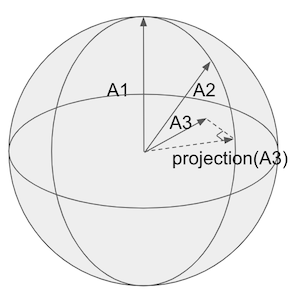
The projection is just the other part of the triangle created by the ‘leftovers’ and An itself.
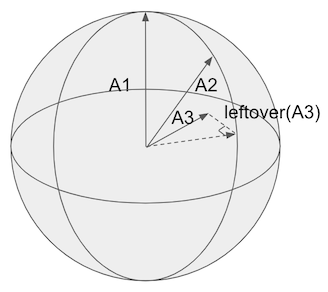
Like thanksgiving, these leftovers are the juicy bits we want 🍗.
If we could find the projection, a little trig can get us θ - the angle between An and its projection - and thus sin(θ) - and viola leftovers 🍰!
How do we find the projection? Luckily there’s an existing algorithm. However, it requires an important input: the vectors describing the A1..An-1 “slice of heaven” span must be made orthogonal to each other.
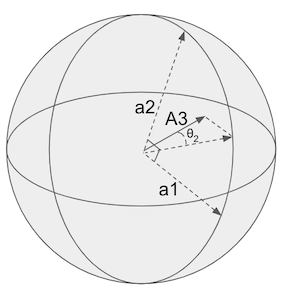
To sum up, we need to follow two steps:
- Go from our not orthogonal span
A1...An-1to orthogonal vectorsa1...an-1that also describe it. - Run the projection algorithm of An or each
a1..an-1
There are many great articles describing each of these steps in isolation. We’ll not get into the weeds of each algorithm. But let’s walk through implementing each step in Python at a high level.
To orthogonal vectors on span
Smart math people have gifted us algorithms for getting orthogonal vectors for a span. For example Gram Schmidt. There’s also a magic process in linear algebra called QR decomposition that does this for us (under the hood it runs an algorithm like Gram Schmidt for us).
QR decomposition turns a column matrix of our A1..An-1s into Q and R. We, care only about Q - it holds the vectors on the span orthogonal to each other. (Sorry R 😭.)
It’s a nice one liner for lazy programmers like me:
Q, R = np.linalg.qr(A) # A here each column is A1...An-1
Now each column of Q are orthogonal vectors still in A1..An-1’s slice of heaven:
Columns of Q:
| a1 | a2 | … | an |
|---|---|---|---|
| a1[0] | a2[0] | … | … |
| a1[1] | a2[1] | … | … |
| … | … | … | … |
Getting the projection
The projection of unit vector a onto unit vector b:
def project_one(a, b):
"""Project a -> b ."""
return b * np.dot(a, b)
(Be sure to see the definition for NON unit vectors, as we have to divide by b’s dot product with itself)
Then to get the full projection for all vectors in a1...an we subsequently add each projection:
projection = []
for a in Q.T:
projection.append(project_one(v, a))
proj = sum(projection)
With the vector proj, we can get the angle between vectors proj and An though their dot product. And add delicious leftovers🥪 to our u.v dot product estimate:
theta = math.acos(np.dot(proj, An))
u.v = A1.u*A1.v + ... + sin(theta)*An.u*An.v
Nice, we can repeat this process for as many reference points as we have!
The next question, how accurate of a dot product can we get? And how many reference points would it require?
(The code here, with tests, can be found here )
Enjoy softwaredoug in training course form!
20% off through December 19, 2025 with code ps5
 I hope you join me at Cheat at Search with LLMs to learn how to apply LLMs to search applications. Check out this post for a sneak preview.
I hope you join me at Cheat at Search with LLMs to learn how to apply LLMs to search applications. Check out this post for a sneak preview.
