Given three unit vectors u, v, and A - can we estimate the dot product of u.v if we only know u.A and v.A? Or put graphically:
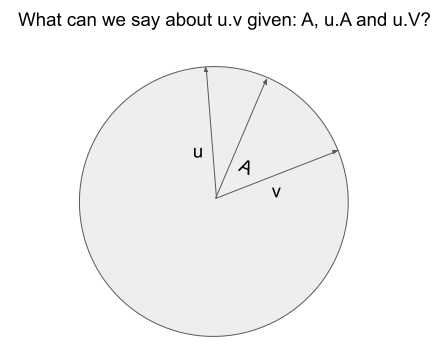
Well let’s take a stab at it. If we could solve this problem, it might have applications for a vector similarity system. We could have a shared reference point, A, store only A and the dot products to A, and use this to make estimates of their similarity to query vectors.
First step - if we don’t actually know u or v, only their dot products to A, to see all possible u and v values we need to think of them as more of a trace in the vector space. This trace corresponds to the set of all possible u or v that have our known u.A/u.A.
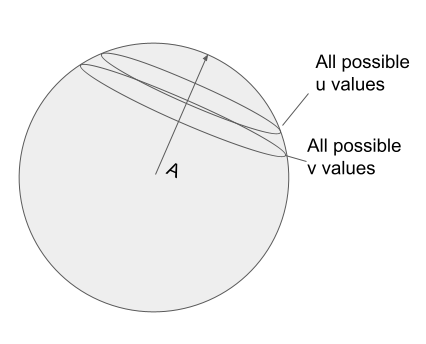
We notice that as u.A and v.A both approach A, the circle shrinks in towards A, and its more likely that u.v is closer to 1.0.
We also notice that the traced circle is the root of the problem. Sometimes u and v might be on opposite sides of their traces. Sometimes they’re close together. Each possibility dictates a different u.v.
Luckily, as u and v converge towards A, the ‘wiggle room’ in these traces shrinks. As u and v converge towards A, we see u.v approach 1.0 - as we’d expect.
But how, mathematically, can we think about u.v?
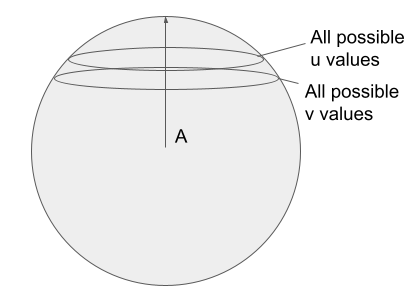
We can rotate this sphere so that A becomes an axis. The 0th dimension corresponds to magnitude each vector has in the A’th dimension. In other words v[0] and u[0] becomes v.A and u.A respectively.
| 0 | 1 | … | n | |
|---|---|---|---|---|
| u | u.A | ? | … | ? |
| v | u.A | ? | … | ? |
Now what’s leftover - dimensions 1..n - are the trace we observe. We notice this is, itself, a sphere - and not a circle - at higher dimensions. I’ll just denote this leftover vector as u1 and v1:
| 1 | … | n | |
|---|---|---|---|
| u1 | ? | … | ? |
| v1 | ? | … | ? |
We can then breakdown u.v as:
u.v = u.A * u.V + u1.v1
We know from a previous post - u1.v1 can be expected to be orthogonal at high dimensions - in other words 0 - which means u.v actually tends to approache u.A * v.A. Note this property remains true even though u1 and v1 are not unit vectors.
On the surface, this seems really useful! It’s also the case, however, that u.A * v.A, would also be expected to approach 0. Unless, of course, we’re cherry picking useful reference points, A in our dense vector space.
Of course, double check my math I could be wrong :).
Enjoy softwaredoug in training course form!
20% off through December 19, 2025 with code ps5
 I hope you join me at Cheat at Search with LLMs to learn how to apply LLMs to search applications. Check out this post for a sneak preview.
I hope you join me at Cheat at Search with LLMs to learn how to apply LLMs to search applications. Check out this post for a sneak preview.
