We expect two n-dimensional vectors to be orthoginal.
In other words, having a dot product of 0.9 does not mean “10% of random vectors have dot products > 0.9”. It’s actually exceedingly rare at high dimensions to be so similar. We similarly expect a dot product of 0.1 to occur much much more frequently.
To make the dot product useful in vector simalirity systems, we need to know what information the dot product conveys. Let’s see if we can compute the probability of observing dot products. In other words, can we quantify the intuition in this table?
| Dot Product | Expected (Intuitive) Prob |
|---|---|
| > 0.9 | Very rare (like <0.01?) |
| > 0.1 | Very common (like < 0.45?) |
It turns out yes! We can do this by computing the ‘polar cap’ area of the sphere compared to the overall area of the sphere. Obviously a tiny ‘polar cap’ area is much smaller than the ‘cap’ formed by a much larger angle. As shown below
To compute the probability, we just need to compute the ratio of the cap area of the whole hypesphere. Luckily, a paper from S. Li helps us out with the math.
N Dimensional Sphere Area
First we need to compute the surface area of an n-dimensional sphere, given by the following. (We can ignore radius r because we’re dealing with unit spheres.)
Here Γ is the gamma function.
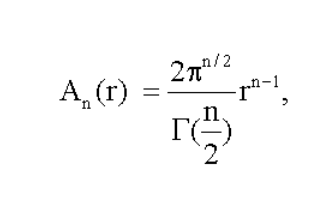
from scipy.special import gamma
from math import pi
def n_sphere_area(n: int):
numerator = 2 * (pi ** (n / 2))
denominator = gamma(n/2)
return numerator / denominator
n_sphere_area(3)
Which gives a surface area of 12.566370614359174 for 3 dimensions.
Cap area, dimensions N given angle theta
Now to compute the area of a cap, which is:
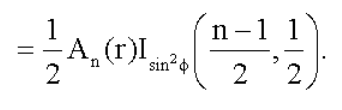
Here I is the regularized incomplete beta function and An is the area of the N-sphere we just defined.
from scipy.special import betainc
from math import sin
def n_cap_area(n: int, theta: float):
sphere_area = 0.5 * n_sphere_area(n)
sin_squared = sin(theta) ** 2
return sphere_area * betainc((n-1)/2, 0.5, sin_squared)
# Ninety degrees should be half the sphere
assert n_cap_area(3, pi / 2) / n_sphere_area(3) == 0.5 # With caution for floating point error
n_cap_area(3, pi / 2) / n_sphere_area(3)
As expected, this outputs 0.5. A cap that goes all the way to the equater covers 50% of the surface area.
Dot product area
Now we just need to change our code to take dot products instead of angles. We do this by taking the arccos of the dotproduct to get an angle. As the dot product is given by:
u . v = |u| |v| cos(theta)
Since these are unit vectors, we can ignore |u| and |v|, and just take the arccos:
from math import acos
def dot_prod_area(n: int, dot_product: float):
theta = acos(dot_product)
return n_cap_area(n, theta)
assert dot_prod_area(3, 0.0) == n_cap_area(3, pi / 2)
dot_prod_area(3, 0.0)
Since a dot product of 0.0 means “orthoginal” - which is the same 90 degrees or pi / 2, we also expect this to give us half the sphere’s surface area. Indeed we get 12.566370614359174 / 2 or 6.283185307179587.
Dot product probability
With cap area and sphere surface area, we have all the ingredients we need!
Probability a dot product is dot_product or above is the ratio of dot_prod_area (ie cap created by that dot product) to the area of the n-sphere:
def dot_prod_probability(n: int, dot_product: float):
return dot_prod_area(n, dot_product) / n_sphere_area(n)
Some sample runs, for 3 and 300 Dimensions:
| Dot Product | Probability (3D) | Probability (300D) |
|---|---|---|
| > 0.9 | 0.0499999 | 3.8176348880615475e-110 |
| > 0.25 | 0.3749999 | 5.68880013789717e-06 |
| > 0.1 | 0.4499999 | 0.0416313931428 |
It’s shocking how hard it is for 300 Dimensional value to have a similarity of 0.9! Since that’s so exceedingly rare, that similarity would be very meaningful in an embedding space. Even a similarity of 0.1 caries tremendous meaning!
Finally, for completeness…
Just a note that for negative dot products, the algorithm above will give you a ‘cap’ from the bottom of the sphere. Or perhaps these are sphere underpants? Spongebob Spherepants?
We just need to adjust our formula to account for this if we want the area above the sphere. So be sure to invert as follows:
def dot_prod_probability(n: int, dot_product: float):
if dot_product < 0:
return 1.0 - dot_prod_area(n, dot_product) / n_sphere_area(n)
else:
return dot_prod_area(n, dot_product) / n_sphere_area(n)
That’s it! I love this kind of vector search napkin math…! If this interests you, be sure to checkout my ML Powered Search Course which discusses vector search over embedding spaces.
(Post is based on this notebook)


