With the prevalence of embeddings in search and NLP, developers often start by thinking in easy to imagine two or three dimensions. But there are some unintuitive surprises when you get to higher dimensions you don’t encounter readily in lower ones. One of those is frequent orthogonality:
Two random vectors from a high dimensional space are much more likely to be orthogonal than two random vectors in low dimensional space. In other words, similarity is something of an aberration. Two things having nothing to do with each other, much more common.
There’s more mathy proofs out there, but let me give some intuitive explanations.
We think about a unit vector (a vector whose length is 1) as being any point along a circle. In particular there’s nothing particularly interesting about two vectors being 90 degrees apart. It is no more common than being 10 degrees, or 170 degrees apart. A clock can be at 3 o’clock (90 degrees) just as often as its at 12:03 (10? degrees).

But take things up to a 3D sphere, and you might begin to see something interesting. Relative to the North pole, there’s far more land area around the equator, than around the arctic circle.
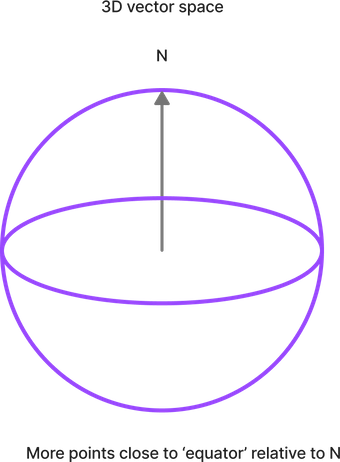
Compare the equator above (90 degrees from N), to the line drawn at 10 degrees away from North:

Wrap a ribbon around the equator, that ribbon will cover more area, than a ribbon wrapped around the tiny 10 degrees ‘arctic circle’.
This isn’t some special property of North. We could make any vector in 3D and we’d see a similar effect relative to that vector’s equator. It’s more likely some point on a globe is on the fat part, not close to our first vector.
But what about the higher dimensions we can’t see?
Well we have to get away from visualizing the dimension, and think of the formal definition of orthogonality. Given two unit vectors u and v, they’re said to be orthogonal if:
u1v1 + u2v2 + … + unvn = 0
And since these are unit vectors, the total magnitude of u or v is no more than one:
sqrt(u1^2 + u2^2 + … + un^2) = 1
Which means the higher the dimensions, the more dimensions our magnitude of 1 gets spread between. It’s diffuse. Few dimensions means the magnitude concentrates in those few components.
Another way to think about it is if we hosted a dinner party. Imagine we poured a pitcher with 1 liter of water between N guests. With two guests (two dimensions), you could, on average, give a pretty healthy amount to each guest’s glass.

Many cups, and you’ll be splitting up that liter of water between many unfortunate dinner party guests:

So that satisfies the unit-vector constraint. These 8 glasses are like the 8 Dimensional vector, u, each with a bit of the ‘magnitude’ split between them. Because they’re diffuse, they will, on average, be closer to empty / 0.
If we look at the dot product constraint we see how hard it is for some other ‘dinner party’ to come up with a similarly poured 8 glasses. That’s what the dot product says after all… to be similar, the dot product approaches 1:
u1v1 + u2v2 + … + unvn
It’s MUCH harder to pour our eight glasses in a similar way than the two glasses. Eight dimensions is hard enough - imagine 768 like BERT models!
It’s much more likely on average, the glasses will be different and closer to empty. This pulls the dot product itself closer to 0 (or orthogonal).
What are the implications of this for embeddings and similarity search over dense vector spaces?
- Because higher dimensions, similarity is harder, more dimensions translates to more precision (the bar gets higher to be similar), whereas in low dimensions orthoginality is mundane (see the sphere and circle above).
- From the vantage point of a single vector, the remaining vector space looks more like a top with many vectors far away, and a very few close. The higher the dimensionality, the ‘pointier’ the top shape becomes, and the fatter the equator.

(Image from this Amazon product
- Focus on close / not orthogonal - When we build similarity systems, we probably care more about those points closest to a ‘query’ vector. Which will be few. And we probably want to ignore/filter out those many many noisy orthogonal vectors that have nothing to do with the query. We care more about accurate similarity estimates of those most similar, nearby, and likely care little about the accuracy of those points ‘muddled’ in the middle near orthogonality.
- Test with real data, not random vectors - When testing similarity systems at high dimensions, we might think randomly generated vectors is good enough, but in reality, this will just create a vector space heavily biased towards orthogonality. It’s important to test with real data!
You can explore this further by trying different vectors in this spreadsheet.
Doug Happenings
Check out my Jan 2023 ML Powered Search Class - Join us and your new best search friends to chat about machine learning, reinforcement learning in search, and the future: vectors and chatGPT!
Enjoy softwaredoug in training course form!
Starting Feb 2!
 I hope you join me at Cheat at Search with LLMs to learn how to apply LLMs to search applications. Check out this post for a sneak preview.
I hope you join me at Cheat at Search with LLMs to learn how to apply LLMs to search applications. Check out this post for a sneak preview.
